Kazık Grupları Nedir? Dikkat Edilmesi Gerekenler Nelerdir?

1)KAZIK GRUPLARI:

Temel elemanı olarak kazıklar nadiren tekil kullanılır. Bir kısım rüzgar türbin temelleri dışında temel seviyesindeki kuvvet çiftleri kazık grupları oluşturularak taşınır.

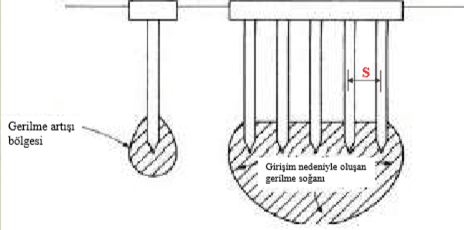
Bir kazık grubunda stabilitenin eşlenik olarak sağlanabilmesi isteniyorsa minimum üç kazık bulunur. Bir kazık grubunda yerleşim planda üniform ve eksenden eksene kazık aralığı eşit olabileceği gibi üst yapı taşıyıcı sistemine bağlı olarak farklı dispozisyonların kullanımı da mümkün olabilir. Tekil ve grup kazık davranışı arasındaki en önemli fark kazık aralığına bağlı olarak grup içindeki kazıklar arasında girişim meydana gelmesi(şekil.1) ve buna bağlı olarak temelin taşıma kapasitesi ve oturma davranışının değişmesidir. Kazık aralığı düştükçe girişim etkisi artar, çok daha derin ve büyük bir zemin kütlesinde gerilme artışı meydana gelir. Kazık grubu veriminin (η) çok düşmemesi için eksenden eksene kazık aralığının S≥3B olması gerekir.

1.1)Grup Taşıma Kapasitesi:

Qp_g=Nkazık * Qp_tekil         (1)                Qblok=Qb_blok + Qs_blok       (2)

Denklem (1) ve (2) kullanılarak hesaplanan taşıma kapasitelerinden küçük olanı grup taşıma kapasitesi, Qgrup, olarak alınır. Yukarıdaki denklemlerde:

Nkazık : Gruptaki toplam kazık sayısı

Qp_tekil : Tekil kazık taşıma kapasitesi

Qb_blok : Kazık grubunda taban taşıma kapasitesi

Qs_blok : Kazık grubunda çevre sürtünme direnci olmaktadır.

 

Grup için güvenlik faktörü Qgrup ve ∑Qyapı kıyaslanarak bulunur:

Fs=Qgrup/∑Qyapı ≥ 3.0

 

Yukarıdaki verilen güvenlik koşulu sağlanmalıdır. Ayrıca gruptaki kazıkların irdelenmesi temel modeli kurulup her bir kazığa gelen yük bulunduktan sonra yapılır. Mühendis temelin blok olarak göçme güvenliğini ve gruptaki her bir kazığın tek tek göçmeyeceğini garanti altına almalıdır.

1.2)Blok sürtünme direnci:

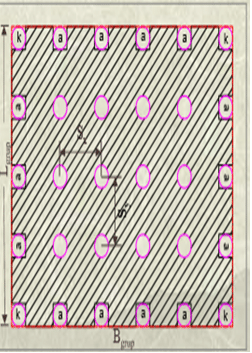
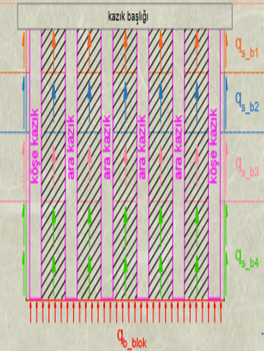
Blok  sürtünme direnci(Qs_blok) gruptaki dış sıra kazıklardan gelen katkı(Qs_bk) ile kazıkların arasındaki toplam zemin katkısının(∑Qs_bz(i)) toplamıdır.(Şekil.2 ve Şekil.3 )

Qs_blok= Qs_bk+ ∑Qs_bz(i)

Qs_bk=4*(Qs_tekil/2)+Na_kazık*(Qs_tekil/4)

Qs_bz(i)=Nara*(S-B)*hi*qs_zemin

(Bu formülasyon x ve y yönlerinde üniform açıklıklar için geçerli olup farklı bir durumda revize edilmelidir.)

Zemin-Zemin sürtünmesinden kaynaklanan birim sürtünme direnci kohezyonlu ve kohezyonsuz zeminler için ;

Kohezyonsuz zeminler:

qs_zemin= K0 * σ’ v_ort * tan Ø

K0=1-sin Ø         (geostatik yanal zemin basıncı katsayısı)

σ’ v_ort : Tabaka için ortalama efektif düşey gerilme

Ø:   içsel sürtünme açısı

 Kohezyonlu zeminler:

qs_zemin=Su

Su: Drenajsız kayma mukavemeti

 

Her tabaka için hesaplanan birim sürtünme dirençleri o tabaka için geçerli yüzey alanı ile çarpılır ve sürtünme direnci hesaplanmış olur. Toplam blok sürtünme direnci tabakalardan gelen dirençlerin toplamıdır.

 

1.3)Blok taban direnci:

Kazık gruplarında kazıklar arası eksenden eksene mesafe iyice açılmadıkça, S>(6-8)B, grubun devasa blok bir temel gibi davrandığı, kazıklar arasında kapsanan zemin kütlesinin grup ile birlikte hareket ettiği kabul edilmelidir. Blok taşıma kapasitesi için Brinch-Hansen taşıma kapasitesi yaklaşımından faydalanılabilir:

qb=0.5* γ’*Bg*N γ*S γ*d γ*i γ*b γ+c*Nc*Sc*dc*ic*bc+ σ’v_uç*Nq*Sq*dq*iq*bq

Bu formülasyonda;

γ’:Taban altında kalan zeminin ortalama efektif birim hacim ağırlığı.

Bg:kazık grubunun taban genişliği

S γ, Sc ve Sq :Şekil faktörleri.                               d γ, dc ve dq:Derinlik faktörleri.

i γ, ic ve iq:Eğik yükleme faktörleri                   b γ, bc ve bq: Taban eğimi faktörleri

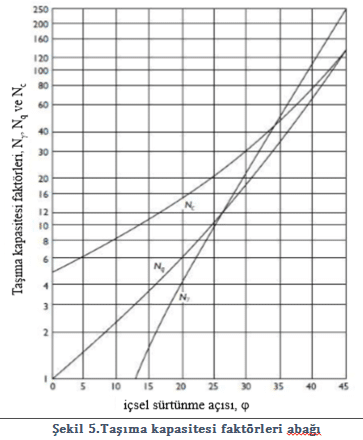
N γ, Nc ve Nq: Taşıma kapasitesi faktörleri

Şekil faktörleri,derinlik faktörleri,eğik yükleme faktörleri ve taban eğimi faktörleri bulunurken literatürdeki şu formüller kullanılabilir;

Taşıma kapasitesi faktörleri bulunurken ise şekil.5 deki abak kullanılabilir;

2) Kazık Gruplarının Oturması:

Kazık gruplarının oturması başlığı altında blok halinde toplam oturma ve grup içindeki kazıkların her birinin yapması beklenen deplasmanlar ele alınacaktır.

Blok oturması hacimsel şekil değiştirmeye (ε_v ), tekil kazık deplasmanı ise daha çok kayma şekil değiştirmesine (γ) bağlı olarak gelişir. Şekil.6’da biri yüzeysel temel ve birisi kısa diğeri uzun kazıklar ihtiva eden iki ayrı temel sisteminden kaynaklanan gerilme dağılımları görülmektedir. Her biri eşit yayılı yük taşıyan üç temelden kazıklı olanlar kazık boyuna bağlı olarak yükü derindeki daha rijit tabakalara aktarmakta, bu sayede toplam oturma miktarını düşürmektedir. Ancak dikkatli olunmazsa kazıklı temeller içinde sığ temellerde görülen oturma problemleri yaşanabilir.

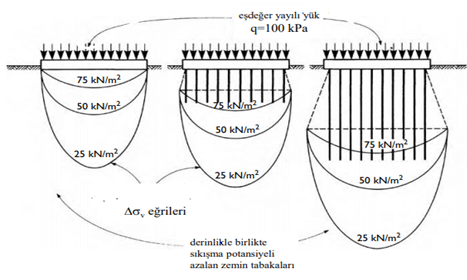
Blok oturmanın hesabına yönelik olarak zemin sıkışma parametrelerinin elde edilmesi için sondajlardan uygun sayıda olanları eşdeğer temel seviyesinin altına doğru B~2B kadar devam etmelidir. Ancak bilhassa 40m derinlikten itibaren Shelby veya Denison tüp ile örselenmemiş örnek alımı pek mümkün olmamakta, bu nedenle sıkışma parametreleri korelatif ilişkiler yoluyla tahmin edilebilmektedir.

Kum veya katı kil içindeki kazık grubunun son çevre sürtünmesi, kazıkların teker teker çevre sürtünmelerinin toplamından daha büyüktür. Öte yandan, kum ve çakıllar içindeki kazık gruplarında, kazıklar arasında kalan zeminin sıkışması sonucu, son taşıma gücü değeri artmaktadır. Bu sonuçlar, kazık grubunun bir ‘blok’ olarak göze alınması ve hesaplanması gerekliliğini doğurmuş, böylece eşdeğer radye kavramı ortaya çıkmıştır .

2.1) Blok Oturma:

Kazık gruplarının blok halinde oturması eşdeğer radye temel seviyesinden itibaren başlar. Eşdeğer radye temel seviyesi zemin profillerinin çoğunda kazık başlığı tabanından itibaren 2L/3 derinliğinde (L: serbest kazık boyu) olmasına rağmen tabakaların durumuna göre bir kısım farklılıklar arz eder.(şekil.7)

 

 

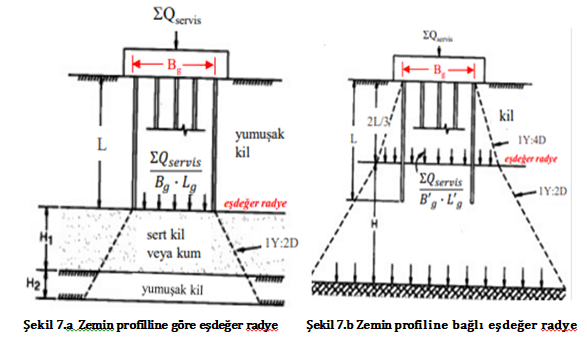
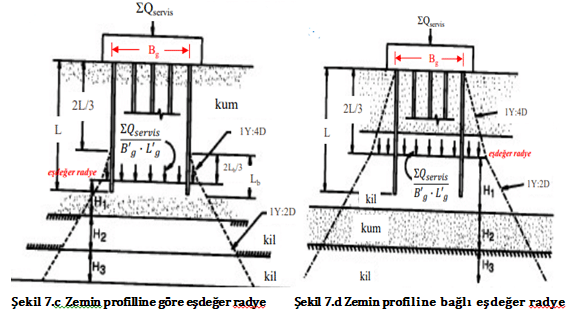
Şekil 7. Zemin profilline göre eşdeğer radye  seviyesinin belirlenmesi   

Eşdeğer radye temel seviyesinin altında kalan tabakaların ortasında gerilme artışı hesaplandıktan sonra bunların sıkışması hesaplanır. Bunların kümülatif toplamı kazıklı temelin toplam oturmasını verir.

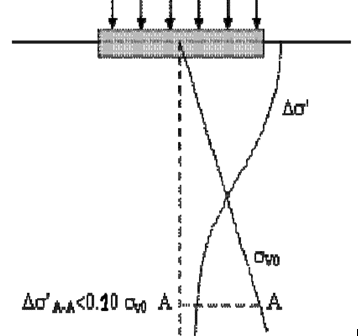
Oturma hesabında dikkate alınacak derinlik, ilave gerilmenin düşey jeolojik gerilmenin % 10’sinden küçük kaldığı seviyedir. Önerilen hesap yönteminde, eşdeğer radyenin derinliğini belirlerken, bu şartın (∆σ’A-A≤ 0.10*σ_v0) sağlanmasına dikkat edilir. Böylece bu seviyeden daha derinde olan zemin, eşdeğer radyeden aktarılan gerilmelerden etkilenmeyecektir.(Şekik.8)

2.2)Konsolidasyon Oturması

Suya doygun kohezyonlu zeminlerde sıkışma parametreleri konsolidasyon deneyinden, bu deneye ait bulgular yoksa korelatif ilişkilerden elde edilir.

Zeminin ön yüklemeli olup olmamasına göre uygun denklem seçilerek tek boyutlu sıkışma teorisine uygun hesap yapılır. Bilahare üçüncü boyut düzeltmesi uygulanır.

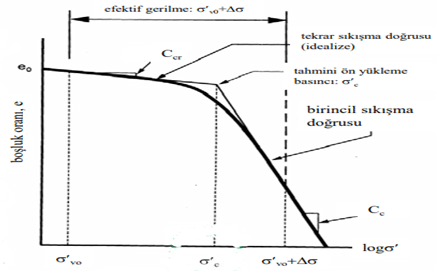
a) Durum I:

Önyüklemeli zeminlerde gerilme artışından sonra tabaka ortasındaki toplam efektif gerilme (inşaat öncesi efektif düşey gerilme [σ’_vo] + üst yapı yükünden kaynaklanan gerilme artışı [∆σ] ) önyükleme basıncından [σ’_c] fazla olursa:

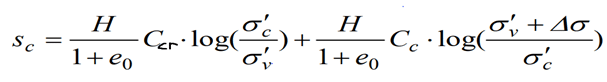
b) Durum II:

Önyüklemeli zeminlerde gerilme artışından sonra tabaka ortasındaki toplam efektif gerilme (inşaat öncesi efektif düşey gerilme [σ’_vo] + üst yapı yükünden kaynaklanan gerilme artışı [∆σ]) önyükleme basıncından [σ’_c] az olursa:

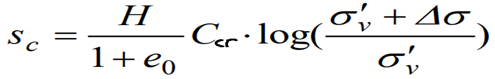
c) Durum III:

Normal konsolide zeminlerde:

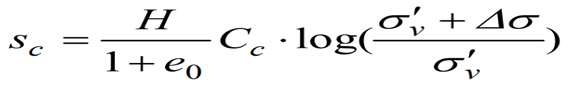
Oturma hesabı hacimsel sıkışabilirlik katsayısı (mv) üzerinden yapılacak olursa s=h*mv* ∆σ bağıntısı kullanılır. İdeal olarak mv efektif gerilme değerine (tabaka ortasındaki efektif gerilme + gerilme artışı: σ’_vo +∆σ) göre seçilir. Ancak zeminden örnek alınamadığı zaman ortalama değer veren korelatif ilişkilerden yararlanılabilir.

2.2.1)Zemin sıkışma parametreleri için korelatif ilişkiler:

Zemin sıkışma parametrelerini (sıkışma indisi: Cc , tekrar sıkışma indisi: Cr , doğal boşluk oranı: e₀ , hacimsel sıkışabilirlik katsayısı: mv , drenajsız deformasyon modülü: Eu , drenajlı deformasyon modülü: E¢) yaklaşık olarak sağlayan ilişkiler laboratuvar veriler ve arazi deney verileri başlıkları altında toplanabilir.

Korelasyonların güvenirliği saha tecrübeleri ve kaliteli örnekler üzerinde elde edilen verilerle kıyaslanmak üzere sınanmalıdır. Bu tür çalışmalar literatürde yaygın olmakla birlikte bir kısmı buraya da alınmıştır. Suya doygun killerde drenajsız kayma mukavemeti (su ) ve deformasyon modülü (Eu veya E¢) arasında geçiş olduğu için su için bir kısım korelasyonlar da bilgi amacıyla eklenmiştir.

 

e-log σ’ eğrisinden çıkarılan parametreler için korelatif ilişkiler:

Cc=0.009*(w_L-10)

Cc= 0.0093*w_n  

Cc =0.00234*w_L*Gs

Cc=1.15*(e₀– 0.35)

Ccr=0.000463* w_L*Gs

Ccr= 0.00194*(Ip-4.6)

Cc=0.141*Gs*(γdoygun/γkuru)^2.4

SPT-N değerinden yola çıkan korelatif ilişkiler:

 

Su=6.25N₆₀ [kPa] (Terzaghi-Peck (1967) )

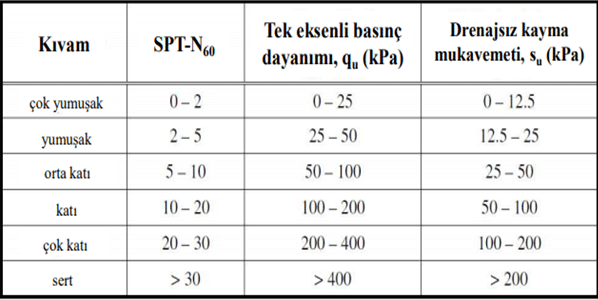
Stroud (1974) korelasyonu genel trendin aksine bu korelasyonda su artan plastisite ile azalmaktadır. Araştırmacı ilerideki yıllarda yapmış olduğu bir yayında bu ilişkinin önyüklemeli killer için geçerli olduğunu beyan etmiştir. Orta plastik killer için Su=4.5N60 alınabilir.

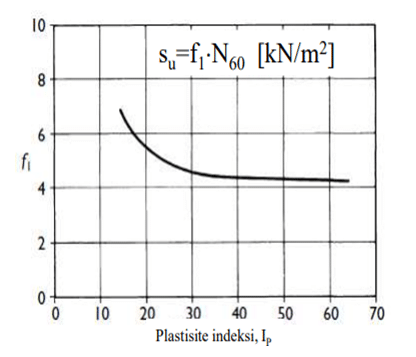
Sowers(1979) tarafından elde edilen su-SPTN60 ilişkisi ise aşağıdaki şekilde verilmiştir:

Arazi deneylerinden bulunan drenajsız kayma mukavemeti kazık taşıma kapasitesi hesaplarında kullanılabileceği gibi zemin deformasyon modülü ve hacimsel sıkışabilirlik katsayısının dolaylı olarak belirlenmesinde de yararlı olabilir.

Deformasyon modülü ile su arasında aşağıda gösterilen yollardan biri izlenerek ilişki kurulabilir:

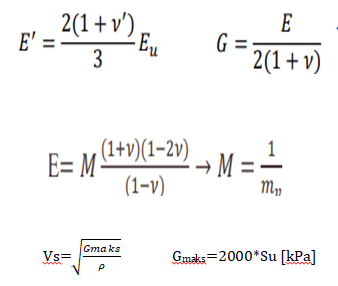
(Örneğin SPTN verileri ile su değerini bulup,daha sonra G’yi hesaplarsınız burdan poisson oranınıda(şekil.13) işin içine katarak E yi çekersiniz ve formülasyondan M ‘yi dolayısıyla mv’yide elde etmiş olursunuz.)

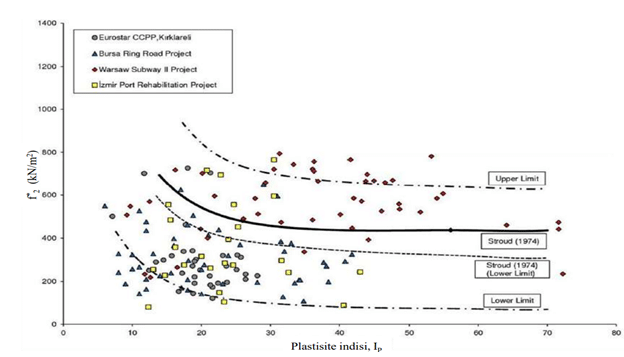
Hacimsel sıkışabilirlik katsayısı üzerine arazi deneyleriyle ilgili bilinen tek korelasyon Stroud (1974) tarafından geliştirilmiş olan ilişki ve bunun üzerine eklenen veri gruplarına dayanılarak çizilen alt ve üst sınır eğrileridir. Mühendis bu eğrileri dikkatli kullanarak mv=1/(f* ₂ ×N60) [m2 /kN] değerlerini tahmin edebilir.

Katı killerde f* ₂=400 alınabilir. Yumuşak killerde ise katsayının f* ₂=150~300 aralığında olması beklenir.

2.3) Kohezyonsuz Zeminlerin Sıkışma Parametrelerinin Tahmini:

Kohezyonlu zeminlerin aksine kohezyonsuz zeminlerin sıkışma parametrelerinin arazi deneyleri yoluyla tahminine yönelik çok daha fazla korelatif ilişki vardır. SPT ve CPT deneyleri örselenmemiş örnek alınamayan kohezyonsuz zeminler hakkında geniş bir veri tabanı oluşmasına yardımcı olmuştur.

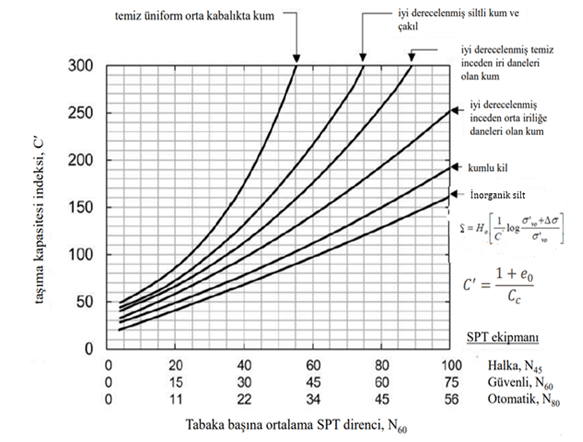
Literatürde mevcut pek çok yöntem arasında Hough Yöntemi (1959) kullanım kolaylığı ve sıkışma indisi (Cc ) ile (e0 ) parametrelerini birleştirmesi açılarından tercih nedeni olabilmektedir. Orijinal Hough abağı (Cc ve e0 parametrelerinin kombine edildiği taşıma kapasitesi indeksi, C¢, parametresinin seçildiği) bilahare Cheney ve Chassie (2002) tarafından modifiye edilmiş ve oturmaların olduğundan fazla hesaplanma durumu bir nebze düzeltilmiştir. Bu yöntem normal konsolide kumlara uygulanabilir.

Kumların önyükleme durumunun belirlenmesinin çok güç olduğu dikkate alındığında kum tabakaları için yapılan hesapların güvenli tarafta kaldığı anlaşılacaktır.

Hough yönteminin dışında kohezyonsuz zemin tabakalarının oturması için BurlandBurbidge (SPT tabanlı) veya Schmertmann (CPT tabanlı) yöntemlerinden uygun görülen birisi de kullanılabilir. CPT ekipmanının 40m’den daha derine pek inemediği dikkate alındığında derin kazıklarda Schmertmann yönteminin fazla kullanım alanı bulamayacağı düşünülebilir.

2.4.) Grup kazık deplasmanı:

Bir kazık grubu içindeki kazıkların maruz kaldıkları eksenel yükler altında göstereceği deplasmanların hesabı temel alanı içindeki farklı oturmanın ve buna bağlı gelişecek iç kuvvetlerin kontrol altına alınması için çok önemlidir. Temel kazıkları birbirine göreceli olarak izin verilen sınırların ötesinde deplasman yaparsa önce kazık başlığında, bilahare üst yapıda çatlak şeklinde hasar meydana gelecektir. Rölatif deplasman için hasar sınırı açısal distorsiyon parametresi (b) ile ifade edilir ve üst yapı proje müellifinin daha düşük bir talebi olmadıkça b≤1/500 koşulunun sağlanması beklenir:

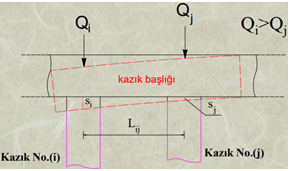
b=Dsij/Lij≤1/500

Dsij=si-sj Dsij : ‘i’ ve ‘j’ numaralı kazıklar arasındaki oturma farkı

Lij : ‘i’ ve ‘j’ numaralı kazık merkezleri arasındaki mesafe

2.5)Killer İçin Ani Oturma:

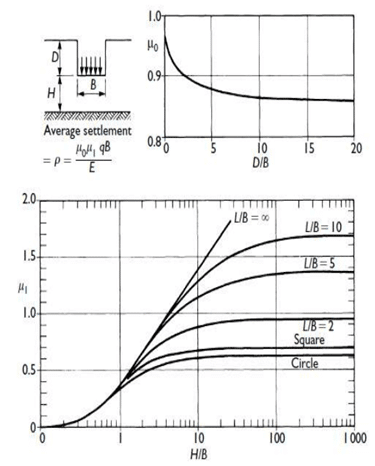
Burada temelin zemin yüzeyinden derinliği D ve tabaka kalınlığı H olurken Ц₁ şekil düzeltmesi, Ц₀ ise derinlik düzeltmesidir. Temelin genişliği B ve uzunluğu L için grubun temel taban seviyesindeki Bg ve Lg plan boyutlarından yola çıkılacak, derinlikle birlikte zâhiri temel boyutları hesaplanacaktır.

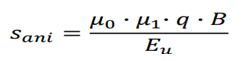
Temel plan boyutları zâhiren gittikçe büyüdüğü için değme basıncı ‘q’ da gittikçe azalmış olacaktır. Denklemdeki E parametresi ani oturma için drenajsız kayma modülü Eu olarak alınmalıdır. Bu durumda Poisson Oranı ѵ=0.5’dir.

2.6)Oturma Düzeltmeleri:

Tek yönlü konsolidasyon sıkışması her tabaka için belirlendikten sonra hesaplanan kümülatif oturma öncelikle ‘derinlik düzeltmesi’ denilen bir katsayı (Ц_d) ile çarpılır:

Bulunan s’ şekil düzeltmelerini de içeren ve gerçek saha uygulamaları ile hesaplanan oturmaları uyumlu hale getiren son bir düzeltmenin daha yapılması gerekmektedir. Skempton ve Bjerrum bu düzeltmeyi içeren katsayıya jeolojik faktör (Цg ) ismini vermiştir.

Bu faktör aşağıdan alınabilir:   

 

 

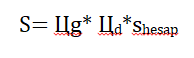
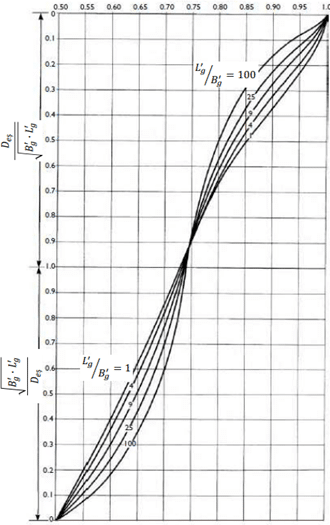
2.7)Nihai Oturma:

Sonuç olarak bir kazıklı temelin nihai oturması:

S_t=ƩS_kum+[ƩS_ani+ Цg* Ц_d*s_hesap]_kil

Şeklinde ifade edilebilir.

 

3)Kazık Gruplarında dikkat edilmesi gereken hususlar;

1. Yumuşak killerde çakma kazık (veya çakma-yerinde dökme) uygulaması yapıldığında zeminin yoğrulacağı, pozitif aşırı boşluk suyu basıncı gelişeceği ve bu nedenle gruptaki dış sıra kazıklar üzerinde negatif sürtünme direnci (Qn) gelişeceği unutulmamalıdır. Zemin çok yumuşadığı için kazıklar arasında kalan zemin ile dışarısı arasında zemin-zemin sürtünmesi hemen devreye girmeyecektir. Temele servis yükü bu tür zeminlerde hemen aktarılmamalı, mümkünse 30 ila 60 gün arası zaman geçmesine fırsat tanınmalı, bu yaklaşım mümkün olmazsa hesaplar ve proje uygun bir şekilde hazırlanmalıdır.
2. Sondaj kazıkları katı-fisürlü killerde bir miktar yumuşamaya neden olur. Bu husus tekil kazık taşıma kapasitesi hesabında dikkate alınmış olmalıdır.
3. Sondaj kazıklarında kazık ucu yumuşaması ve benzeri etkilerin blok taşıma kapasitesi üzerinde fazlaca bir önemi olmaz (kazık yükleri süperpoze olarak çok daha derin bir zemin kütlesini kapsar). Ancak grup içindeki her bir kazığın performansı ayrıca teminat altına alınmalıdır.
4. Kazıklar imal edilirken bunların imalat toleranslarını mutlaka sağlaması gerektiği unutulmamalıdır. Teknik şartnamesinde daha düşük sınırlar belirtilmediği takdirde bir kazığın projesindeki yerleşim planına göre merkez koordinatındaki sapma miktarı her yönde en fazla 75mm olabilir. Düşey imal edileceği belirtilmiş olan kazıklarda düşeyden sapma en fazla 1/75 olabilir. Ancak yüksek yapılarda kazık boyu uzayacağı ve kazıklar birbirine yaklaşacağı için düşeyden sapma toleransı 1/200 değerine kadar düşürülebilir. Kazı imalat makinelerinde hassas eğim ölçerlerin bulunması bu açıdan (düşeylik kontrolü) zorunludur. Eğik projelendirilen kazıklarda proje eğiminden izin verilen sapma istenilen eğim en fazla 1Y:6D ise 1Y:25D, proje eğimi 1Y:6D’den büyük ise 1Y:15D olabilir.
5. Kazıklar arası eksenden eksene mesafenin S≥3B koşulunu sağlamasına dikkat edilmelidir. Küçük çaplı kazıklarda ayrıca S>(100cm+B) koşulu da yerine getirilmelidir.
6. Karstik veya maden galeri boşluğu (örneğin Zonguldak ve benzeri yerleşim yerleri) içerme ihtimali olan jeolojik formasyonlarda mutlaka jeofizik tomografi serimleri yapılmalıdır.

 

NOT:  Bu yazının kaynağı, Prof. Dr. Gürkan Özden’in Özel Temeller Ders Sunusu’dur. İçeriği oluştururken; metin, şekil, tablo ve görseller için kendisinden özel izin alınarak hazırlanmıştır.