Mütemadi kirişlerin veya kat çerçevelerinin değişik yüklemeler altında düşey yükler için hesabını yapmada kullanılan yöntemlerden biridir. Metodun pratikliği, hareketli yük değişimini dikkate alarak açıklık ve mesnet momentlerinin maksimum değerlerini bir kerede hesaplayabilir.
Bu yazıda Yapı Statiği‘nde anlatılan ve Betonarme dersinin önemli noktalarından biri olan Biro Metodu sorularının çözümü hakkında bilinmesi gereken hususları sizlerle paylaşacağız. Hazırsanız başlayalım.
NOT
Burada yer alan maddeler, Fırat Üniversitesi İnşaat Müh. Ders Notları esas alınarak hazırlanmıştır. Soru tipleri ve soru çözüm aşamaları değişkenlik gösterebilir.
Konuya girmeden önce ankastre uç moment ve dağıtma sayılarının bulunması hakkında probleminiz olmamalıdır.
- Soruya ilk olarak redör hesaplamalarıyla başlanır. Cross metodundaki hususları tekrar hatırlayalım:
• Sabit mesnetli kolonda relatif redör alınır. (Kx0,75)
• Hareketli mesnetli kolonda redör sıfırdır.
• Ankastre mesnetli kolonda redör normal bulunan değerdir.
• Konsolda redör sıfırdır.
• Dağıtma sayısı 1 olan mesnedin karşı mesnedinde relatif redör alınır. ANCAK biro metodunda daha yaklaşık değer bulunmak istendiği için bu kural geçerli değildir. - Redör hesaplamaları tamamlandıktan sonra dağıtma sayılarının hesaplanmasına geçilir. Herhangi bir noktanın dağıtma sayısı hesaplanırken o noktanın redörü o bölgedeki tüm redörlerin toplamına bölünür.
- Ankastrelik uç momentlerin hesaplanması kısmına geçilir. Cross metodundan farklı olan önemli hususlardan biri de sağ ve sol momentlerin işaretidir. Cross metodunda sağdaki momentlerin önüne (-) koyulurken burada bütün momentler (+) alınır ve en son işlemde işaretler değiştirilir.
GERİ KALAN DETAYLARI SORU ÜZERİNDE İNCELEYECEĞİZ.
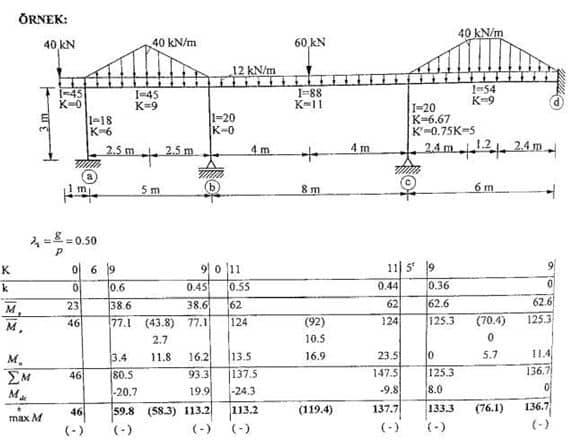
4. Sorunun başında yer alan λ sayısı ölü yüklerin toplam yüklere oranıdır. Hesaplanan uç momentler bizim Mp satırımızı yani toplam yükümüzü oluştururken bu sayıları λ sayısı ile çarptığımızda Mg satırındaki ölü yükleri bulmuş oluruz.
5. Mg ve Mp satırlarımızı doldurduktan sonra Mp satırında açıklık ortası momentleri bulmamız gerekir. Bu değerleri bulmamız için de çarpım tablosundaki formülleri kullanırız. Bakmamız gereken formüller M0 formülleridir.
6. Mn satırını yani nakil momentlerini hesaplama kısmına geçilir.
Örneğin 3,4 değerinin hesabı şöyle yapılır: (77,1- 62) = 15,1; 15,1 x 0,45 = 6,8 ; 6,8 / 2 = 3,4
Mesela aynı satırdaki 23,5 değerinin hesabı : (124 – 38,6) = 85,4 ; 85,4 x 0,55 = 47 ;47/2=23,5
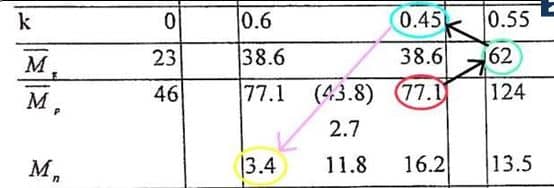
7. Mn(nakil momentler) hesaplandıktan sonra bu değerlerin açıklığa katkıları hesaplanacaktır. Nakil momentler, dağıtma sayılarının 1 fazlasıyla çarpılıp 2’ye bölünür. Mesela 3,4 değeri için hesaplarsak; 3,4 x (1 + 0,6) = 5,4 ; 5,4 / 2 = 2,7
8. Artık ∑M satırını doldurmak gerekir. Bunun için Mp ve Mn satırları toplanır. Açıklık ortasındaki değerlerin toplanması en sonda yapılacaktır.
9. ∑M değerleri bulunduktan sonra Mde satırına geçilir.
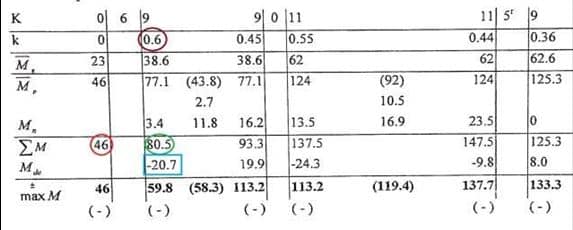
Bulacağımız değer için yapılacak işlem özetle şudur; Bulacağımız değerin olduğu noktada sonraki ∑M değerinden olduğumuz yerdeki ∑M değeri çıkartılır ve o noktanın dağıtma sayısıyla çarpılır.
Mesela -20,7 nin hesabı >>> 46 – 80,5= -34,5 ; -34,5 x 0,6 = -20,7
Mesela 19,9 değerinin hesabı >>> 137,5 – 93,3 = 44,2 ; 44,2 x 0,55 = 24,3
10. Mde değerleri de hesaplandıktan sonra son olarak max M değerlerinin hesaplanmasına geçilir. Bu satır doldurulurken ∑M değerleriyle Mde değerleri toplanır. Bu satır doldurulurken açıklık ortası momentler de bu satıra yazılır. Açıklık ortası momentler yazılırken nakil momentlerin açıklığa katkısı olarak hesapladığımız değerler de toplanarak yazılır.
Örneğin (58,3) açıklık ortası değeri [43,8 + 2,7 + 11,8] işlemiyle bulunmuştur.
11. Max M değerleri bulunduktan sonra açıklık ortası değerleri hariç bulunan tüm değerlerin işaretleri değiştirilir.
NOT: BU İÇERİK, KAYNAK GÖSTERİLMEDEN PAYLAŞILAMAZ.
Sanal Şantiye sitesinden daha fazla şey keşfedin
Subscribe to get the latest posts sent to your email.