Demiryolu altyapısına ve üstyapısına gelen dinamik etkileri hesaplamak için, dünyada kullanılan çeşitli yöntemler;
Bunlar;
1)STATİK YÖNTEM
2)QUASİ – STATİK YÖNTEM
3)DİNAMİK ANALİZ
Statik yöntemde hat üzerindeki katarın etkisi dinamik değil, statik bir yük olarak kabul edilir.
Quasi-Statik Yöntemde durağan olarak hesaplanan kuvvetler bir dinamik etki katsayısı ile çarpılarak kullanılır ve böylece statik olarak hesaplanmış yükler dinamik bir etki olarak hesaba katılır.
Dinamik Analizde ise hat üzerinde hareket eden trenin, hat üzerindeki etkileri dinamik olarak modellenir ve bu değerlere göre boyutlandırmalar yapılır. Bu yöntemler arasında en iyi sonucu “Dinamik Analiz” vermesine karşın, bu yöntemde bir model oluşturmak zor ve hesaplar Quasi-Statik Yöntem’e göre daha zordur.
STATİK YÖNTEMLE DÜŞEY YÜK HESABI
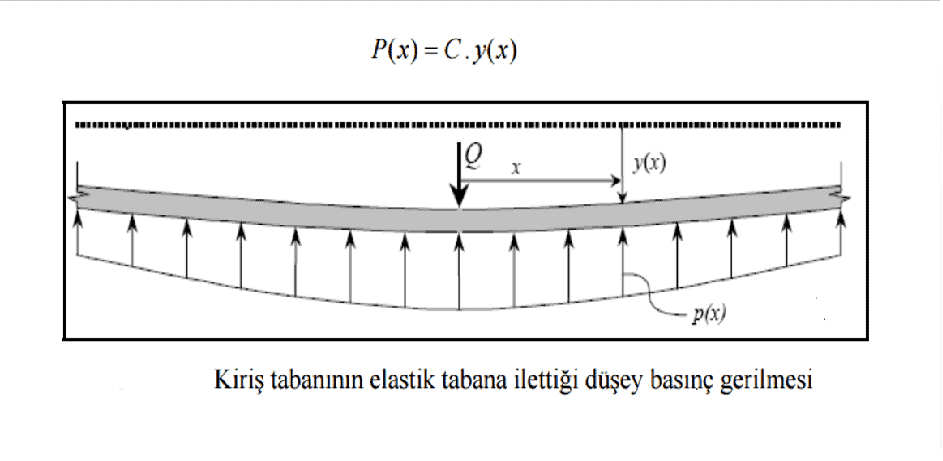
Üstyapı elemanlarının düşey dinamik dingil yükleri altındaki zorlanmalarının araştırılmasında kullanılan en yaygın yöntem, Winkler’in geliştirmiş olduğu ve Zimmermann’ın demiryollarına uyguladığı “Elastik Tabana Oturan Sürekli Kiriş Yöntemi”dir. Winkler hipotezine bağlı olarak şekildeki yol çerçevesi, Zimmermann tarafından traverslerin yük ileten kısımlarının 90 derece döndürülerek, uç uca eklenmesiyle ray ve traverslerden oluşan sanal (hayali) bir sürekli kompozit kirişe dönüştürülmüştür.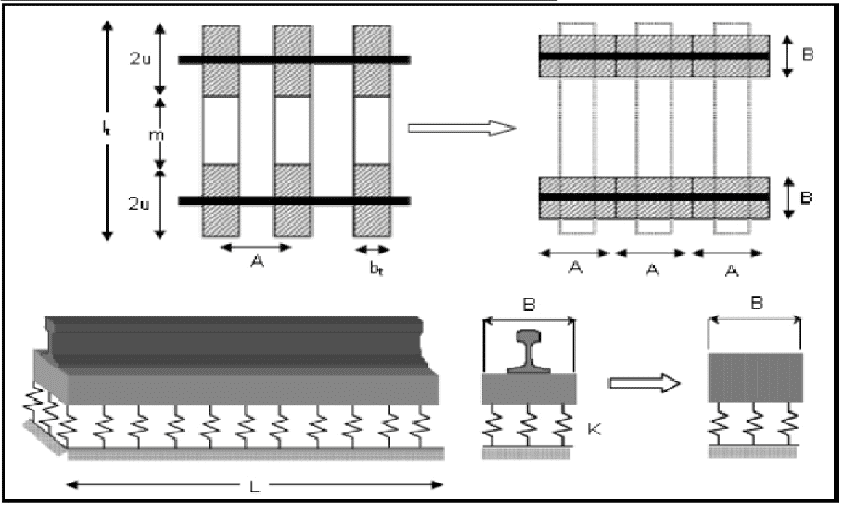
Şekilde ki, “B” sanal kiriş genişliği, “L” karakteristik uzunluk (elastik uzunluk) olarak isimlendirilir. Winkler hipotezine bağlı olarak geliştirilen “Sürekli Kiriş Modeli” için öncelikle sanal kiriş genişliği ve karakteristik uzunluk değerleri elde edilir.
Sanal kiriş genişliği;
B= (2u∗bt)/A
Eşitlikte yer alan “2u” değeri traversin yük ileten kesimlerinin uzunluğu olup; 2u=(lt-m)/2
Şeklinde ifade edilir.
m=ekartman uzunluğu =1432 mm
Kirişin karakteristik (elastik) uzunluğu, ray eğilme rijitliğine, sanal kiriş genişliğine ve elastik tabanın yatak katsayısına bağlı olarak aşağıdaki şekilde hesaplanır.
L=∜(4EI/BC)
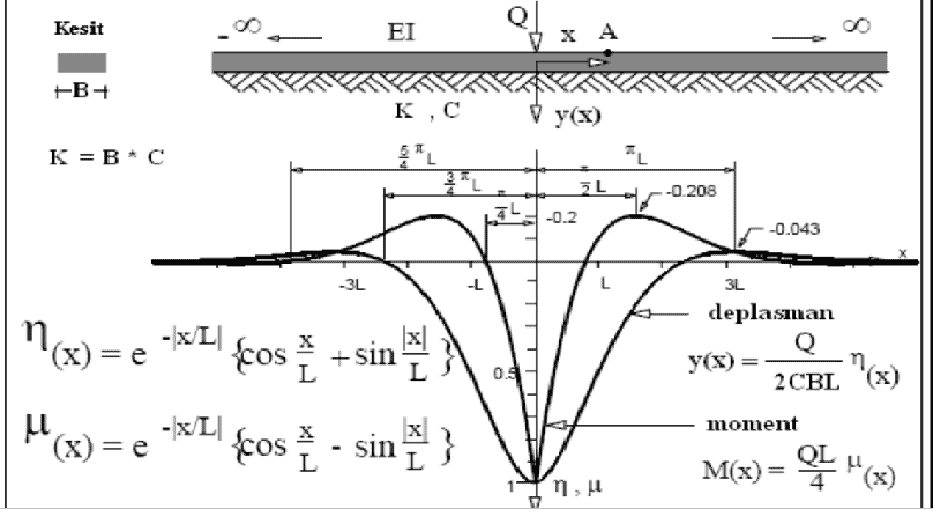
- Q statik tekerlek yükünün etkimesi durumunda kirişin A noktasında oluşacak çökme ve çökme etki katsayısı değerlerine ilişkin eşitlikler;
y(x)=(Q/2CBL)∗η(x)
η(x)=e^(-x∕L) (cos(x∕L)+sin(x∕L))
Q : Statik tekerlek yükü (N)
y(x) : Kirişin (ray ve traversin) A noktasındaki düşey elastik çökmesi (mm)
η(x) : Çökme etki katsayısı
C : Elastik tabanın yatak katsayısı (N/mm^3 )
- Kirişin A noktasındaki eğilme momenti ve moment etki katsayısı değerleri ise;
M(x)=(QL/4)*μ(x)
μ(x)=e^(-x∕L) (cos(x∕l)-sin(x∕L))
M(x) : Kirişin A noktasındaki eğilme momenti (Nm)
µ : Moment etki katsayısı
bilgilerin devamı için slayt dosyasını indirebilirsiniz…
https://drive.google.com/open?id=1CZFCrEyfUO6lPFfFk8EZ4vNmIGwda-v_
